串列與平行多項式演算法（VHDL）

[Kevin_6462]

邏輯主頁

特點

本文涵蓋以下主題：

• 串列和平行實現算術函數方法的比較
• 基本串列乘法和加法的建構區塊
• 基於串列邏輯的整數多項式實現
• 可變多項式階數和資料寬度
• 範例測試平台

介紹

在之前的一篇文章「 使用 Horner’s Rule 霍納規則和定點運算實現多項式（VHDL）」中，我討論了使用霍納規則（Horner’s Rule，或名「秦九韶演算法」）和定點邏輯在更少時脈週期內計算多項式的優勢。在本文中，我們將探討一種截然不同的方法，即使用串列邏輯而非平行邏輯，這種方法需要更多的時脈週期，但面積卻顯著減少，並且可能實現更高的時脈速率。在大多數現代設計中，速度和功耗比面積更重要，但在特殊情況下，串列邏輯仍然值得考慮。另請注意，本設計使用的是全精度整數運算，而不是第一篇文章中的定點運算。

背景

霍納規則（Horner’s Rule）

與上一篇文章一樣，本文使用霍納規則來減少所需的乘法次數。假設我們有一個如下形式的 n 階多項式

f(x) =a_nxⁿ + a_n-1x^n-1 + … +a₁x + a₀.

直接使用此形式計算需要總共 n(n+1)/2 次乘法和 n 次加法，因此計算複雜度為 O(n²)。

霍納規則指出，我們可以將其因式分解，並將多項式重寫為：

f(x) =(((a_nx + a_n-1)x + a_n-2)x + a_n-3)x + … )x +a₀.

使用此形式可將所需的運算次數減少為 n 次乘法和 n 次加法。計算複雜度現在降至 O(n)，使高階多項式更易於管理。

串列運算

由於多項式是乘法和加法的組合，因此本設計中的兩個主要構建區塊是這些函數的串列版本。第一個也是最簡單的區塊是加法器。

圖 1. 串列加法器框圖。

串列加法器其實就是一個全加器，帶有一個用於進位的回授觸發器和一個用於輸出的觸發器。因此，如果 A 為 M-bit，B 為 N-bit，則完整的加法運算需要 max(M,N) 個時脈週期。

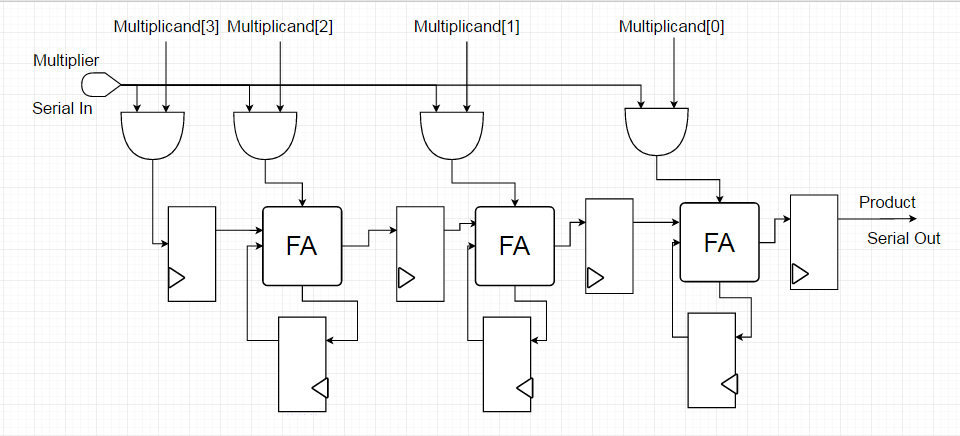
圖 2. 4-bit 串列乘法器範例。

此圖展示了一個 4-bit 串列/平行乘法器範例。其中一個輸入是平行的，儲存在暫存器中，另一個輸入是單一位，以串列方式提供。AND 閘產生部分積，這些積與前一級的輸出一起送入加法器。每個加法器的進位輸出透過觸發器回授到其進位輸入端。在操作過程中，從第 0 位元開始向左移動，將一列部分積和進位相加，並將結果位元閂鎖到輸出觸發器中。對於寬度為 M 的被乘數和寬度為 N 的乘數，整個乘法需要 M+N 個時脈週期。

在本設計中，加入了一點額外的邏輯來處理負數的情況。如果乘數為負，則將其變為正數，然後對最終結果取反。這確保了結果始終能夠正確地進行符號擴展。

乘法器和加法器組合成更高等級的乘加區塊，實現函數 Ax+B。需要一個額外的觸發器來延遲 B 輸入，使其在正確的時間到達加法器。

運作
在頂層，串列多項式區塊由多個與多項式階數相等的乘加區塊、兩個用於輸入和輸出的移位暫存器以及一個控制資料流的狀態機組成。圖 3 顯示了三階多項式資料路徑的簡化視圖，其中省略了一些額外的控制訊號。請注意，粗線表示總線，普通線表示單一位元。

圖 3. 串列多項式區塊的頂層視圖。

輸入和輸出

多項式區塊有兩個通用參數，分別用於指定輸入資料的寬度和它所實現的多項式的階數。

載入輸入移位暫存器有兩種方式，可以透過 s_p 訊號切換。如果 s_p 為高電平，X 暫存器將透過 shift_X 連接埠串列載入。如果 s_p 為低電平，X 暫存器將在下一個時脈上升緣平行載入。

coeffs 向量為每個系數包含一位，其中 coeffs(0) 表示 a_n 的串列線路，coeffs(1) 表示 a_n-1 的串列線路，以此類推。對於從 an-2 開始的每個系數，在輸入和加法器之間添加兩個觸發器，之後的每個系數都會添加兩個觸發器。這會延遲訊號，使其在正確的時間到達相應的區塊。這些觸發器由主時脈訊號的反相時脈驅動，以最大限度地延長後續階段的建立時間和保持時間。

在輸出端，結果可以從 shift_out 連接埠或平行結果連接埠取得。每個連接埠都有一個相應的標誌訊號，用於通知外部主機計算已完成。一旦 shift_out 保持結果的最低有效位元（LSB），Valid 訊號就會被宣告，並保持高電平直到計算完成。一旦完整的結果載入到輸出移位暫存器中，Done 訊號就會被宣告，並在下一次計算開始時被解除宣告。

FSM 控制

圖 4. 狀態機圖。

上圖所示的狀態機用於控制計算流程。在 INIT 狀態下，X 輸入匯流排上的資料被閂鎖到暫存器中。如果使用串列模式，則 shift_X 上的資料將被閂鎖。所有其他控制訊號均設定為其初始狀態。

當 start 變成高電平，狀態機可以切換到 SERIAL_LOAD 狀態或 CALC 狀態。如果選擇串列模式，狀態將切換到 SERIAL_LOAD 狀態，此時數學部分被停用，X 的剩餘位元將被移入輸入移位暫存器。當操作完成後，或如果在 INIT 狀態下選擇了平行模式，狀態將變為 CALC。

CALC 是數學運算的起點。鏈中的第一個乘加區塊被啟用，輸入移位暫存器被停用。在此狀態下，時脈週期會被計數並用於啟用乘加區塊和輸出暫存器。由於乘加運算需要兩個時脈週期，因此鏈中的下一個區塊會在前一個區塊啟用兩個時脈週期後啟用，直到所有區塊都啟用為止。經過兩個 poly_order 時脈週期後，計算結果的第一位元（LSB）。此時，輸出移位暫存器被啟用，以便最終結果可以開始移入。

下圖時序圖顯示了對於具有 4-bit 資料寬度的四階多項式，每個階段的結果何時可用。請注意，在計算出每個階段的最後一位元（階段 1，週期 10-11）後，所有後續位元都是結果的符號擴展。

圖 5. 計算過程時序圖。

經過額外的 (poly_order+1)*data_width 時脈週期後，計算最終結果的 MSB 並將其移入輸出暫存器。然後停用輸出暫存器，狀態變成 COMPLETE。

在 COMPLETE 狀態下，最後完成位元被宣告，狀態機回到 INIT 狀態，開始新的計算。

優點及缺點

至此，應該要清楚的是，這種方法比更傳統的平行方法需要更多的時脈週期。那麼一個合理的問題是：如果這種方法速度慢得多，為什麼還有人會使用它？答案在於資源佔用。下表比較了串列和平行拓撲中乘加區塊的 Quartus 綜合結果。平行版本是使用 Altera 目錄中的 IP 建構的，並針對 Cyclone V SoC 進行了預設最佳化。

表 1. ALM 中的資源佔用情況。

雖然平行在低資料位寬下與串列大致相同，但其成本會隨著位元寬的增加而呈現二次方成長。然而，由於大多數 FPGA 晶片上都整合了內置乘法器，因此通常無需使用邏輯元件來實現乘法器。

串列實現的成本會隨著資料位寬的增加而線性增加。但這仍然只在延遲不成問題的情況下才實用。平行乘加法的最小延遲為一個時脈週期，而串列方法的最小延遲為乘積的位寬加一。例如，32-bit 串列乘加法需要 65 個時脈週期。

串列方法是一種有趣但又不常見的解決方案。它適用於透過串列協定從外部主機接收資料的情況。在這種情況下，資料可以在傳入時進行處理，而不必等待整個事務完成。在其他主要考慮面積而非延遲的情況下，也可以考慮串列方法。

模擬與測試

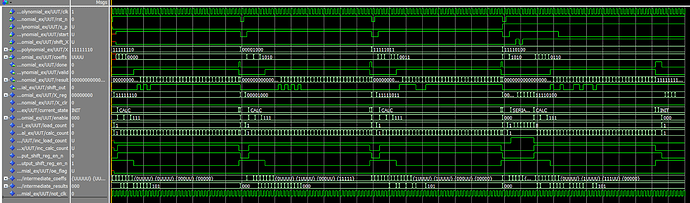
此設計在 ModelSim 中進行了模擬。範例測試平台包含四組隨機選擇的系數值。前三組使用平行載入模式，最後一組使用串列載入模式。

圖 6. 模擬螢幕截圖。

總結

當資源節約是重要因素而延遲不成問題時，串列運算是一種非常有用的選擇。因此，雖然它非常適用於特定情況，但它仍然是一種值得注意的替代方案。由於多項式在工程領域無所不在，因此它是一個很好的起點，可以從串列構建區塊創建更高級的函數。

此概念的可能擴展可以應用於浮點數或定點數。整體多項式設計也可以進行修改，使其完全管線化，從而更有效率地處理連續計算。

下載

.zip 檔案包含該專案的所有 VHDL 原始文件，包括頂層測試平台和用於模擬的 .do 檔案。

Serial Polynomial_v1.1.zip (13.0 KB)