Verilog 程式碼範例
DeBounce_v.v (2.5 KB)
DeBounce_tf.v (1.5 KB)
介紹
註:本頁資訊主要取自另一文章「解彈跳邏輯電路(VHDL)」;設計概念適用於 Verilog 和 VHDL 實作。
在使用者介面中使用機械開關是一種普遍的做法。然而,當這些開關被觸發時,觸點通常會在穩定狀態之前相互反彈或彈開。目前有幾種方法可以解決這種暫時的模糊性問題,包括使用硬體或軟體。本文,我們將討論如何使用一個簡單的數位邏輯電路來解決這個問題(這是 FPGA 或 CPLD 與按鈕或其他開關介面時的常見任務)。本文包含解彈跳模組和測試夾具的通用 Verilog 程式碼。
工作原理
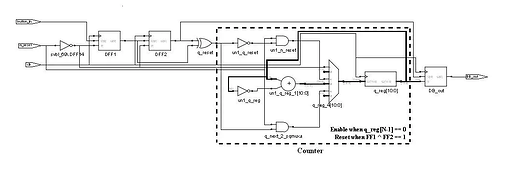
圖 1 展示了本文討論的解彈跳電路。此電路持續將按鈕的邏輯電平輸入 FF1,然後輸入 FF2。因此,FF1 和 FF2 始終儲存按鈕的最後兩個邏輯電平。當這兩個值在指定時間內保持相同時,FF3 將啟用,並將穩定值輸入到結果輸出。
互斥或(XOR)閘和 N-bit 計數器完成計時。如果按鈕的電平發生變化,FF1 和 FF2 的值會相差一個時鐘週期,並通過 XOR 閘清除零 N-bit 計數器。如果按鈕的電平保持不變(即 FF1 和 FF2 的邏輯電平相同),則 XOR 閘會釋放計數器的同步清除訊號,計數器開始計數。計數器將繼續以此方式遞增,直到 (1) 達到指定時間並啟用輸出暫存器,或 (2) 由於按鈕的邏輯電平尚未穩定而被 XOR 閘中斷並清除。
計數器的大小決定了驗證按鈕穩定性所需的時間。當計數器遞增到其進位輸出位元被置位的程度時,它會停用自身繼續遞增,並啟用輸出暫存器 FF3。電路將保持此狀態,直到另一個按鈕值輸入到 FF1,並通過 XOR 閘清零計數器。
圖 1. 解彈跳電路
計數器大小
計數器的大小和時脈頻率共同決定了驗證按鈕穩定性的時間週期 P。公式 1 描述了這種關係。

在典型的應用中,時脈週期數很大,因此可以安全地忽略載入 FF2 和 FF3 的額外兩個時脈週期。
大多數開關在觸發後 10ms 內達到穩定的邏輯電平。假設我們有一個 50MHz 的時鐘,我們需要計數 0.01*50,000,000 = 500,000 個時脈週期才能達到 10ms 的穩定時間。一個 19-bit 計數器可以滿足這項要求。使用計數器的進位輸出引腳(如圖 1 所示)無需評估計數器的整個輸出匯流排。使用此方法,實際實現的時間為 (219+2) / 50,000,000 = 10.49ms。
解彈跳通常不需要很高的分辨率,因此使用進位輸出引腳識別驗證時間所引入的相對較小的誤差足以滿足大多數應用的需求。但是,如果需要更高的時間分辨率,可以對計數器的一些最高有效位元進行邏輯「AND」運算,以最少的額外邏輯開銷實現此目的。
範例程式碼和模擬
此處提供的範例程式碼 DeBounce_v.v 實例化了圖 1 中的電路。參數「N」定義了計數器的大小。圖 2 展示了此設計的模擬結果,其中計數器大小設為 11-bit,或為了方便於表達和易於閱讀,計數設定為 1024。這相當於 2^11/100MHz = 20.48us 的延遲。這對於實際使用來說並不合理,但對於演示目的來說卻非常理想。
圖 2. ActiveHDL 模擬結果
結論
這個簡單的邏輯電路解決了可編程邏輯的機械開關解彈跳問題。
附加資訊
更多設計支援、產品教學、應用筆記、使用者指南和其他文檔,請訪問 Lattice 網站:
http://www.latticesemi.com/dynamic/index.cfm?fuseaction=view_category&source=topnav