程式碼下載
AccelerationLimitedMotorController.vhd (3.9 KB)
AccelerationLimitedPositionControl.vhd (6.2 KB)
cosine.vhd (3.4 KB)
PWMcomparator.vhd (3.3 KB)
UPDOWNcounterANDswitch.vhd (4.6 KB)
介紹
步進馬達作為離散狀態元件,在需要精確位置或速度時極為有用。作為離散狀態裝置,這些馬達特別適合數位系統控制。雖然微控制器適合此類應用,但可編程邏輯元件(PLD)也擁有許多優勢。 PLD 是一種節能且靈活的系統,它還能輕鬆實現片上通訊標準的整合、並行性能以及用於多馬達控制的高引腳數。本文將介紹使用超高速積體電路硬體敘述語言(Very High Speed Integrated Circuit Hardware Description Language,VHDL)對 PLD 進行程式設計以使其用作步進馬達控制器的一些基本注意事項。
背景
步進馬達是一種離散狀態元件。目前使用雙繞組是最典型的方法,因此本文僅討論雙繞組馬達(儘管本文涵蓋的概念很容易推廣到控制多繞組馬達)。
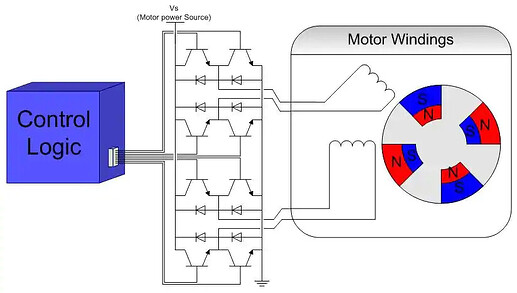
圖 1. 簡化的 45 度雙極永磁步進馬達控制系統。
請注意,兩個相對繞組的間距為磁體圖案重複距離的 1/4;這相當於每個繞組能夠產生 90 度的相移。中間的驅動電路(電晶體)用於處理流經馬達的電流;二極體的作用是保護開關免受電感反沖的影響。
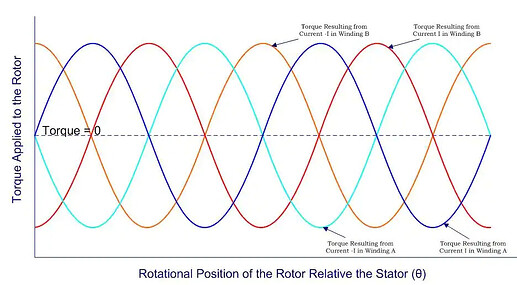
當恆定電流流過馬達的一個繞組時,會產生一個近似正弦的扭矩曲線,其節點固定(圖 2 中的深藍色曲線)。馬達一半的步進出現在曲線的節點上,但只有一半是馬達趨向的最低能量狀態。將電流反向(圖 2 中的青色曲線)將使正弦曲線繞扭矩等於零軸翻轉,最高能量狀態和最低能量狀態將交換;這總是導致馬達大約位於兩個最接近的最低能量狀態的中間位置,因此幾乎無法透過一個繞組來控制馬達。引入第二個繞組後,我們可以控制一個正弦曲線,其節點固定在第一個正弦曲線節點的中間位置(圖 2 中的紅色和橙色曲線)。由於每個繞組的兩條曲線直接相加,因此得到的扭矩與旋轉位置曲線的相位現在是可控的。
圖 2. 在雙繞組馬達中,驅動電流 I 和 -I 通過任何一繞組可能產生的扭力。
請注意,在任意時刻,每個繞組僅產生一個扭矩正弦波。
對於步進循環,我們考慮提供兩個三元變數(每個繞組一個)的可能性。每個繞組的電流分別為 I、0 或 -I,因此共有九種可能性。以特定順序和特定速率循環切換相關狀態,構成了步進馬達的基本控制。如果能夠獲得每個繞組電流的類比值,則可以使它們的振幅以 90 度的相位差進行正弦變化,從而產生更精確的扭矩波供馬達驅動;這種控制方法稱為正弦微步進,其效果與驅動同步馬達相當。
與幾乎所有情況一樣,馬達消耗的電流過大,無法直接連接到任何 PLD。因此,需要外部驅動電晶體來切換流經馬達繞組的電流。必要的外部硬體超出了本應用筆記的討論範圍,因此不予考慮。
關於步進馬達控制硬體的文獻資料非常豐富。想要全面了解步進馬達,Jones 的《步進馬達》是一個易於訪問且隨時可用的資訊來源。
應用
使用 PLD 控制步進馬達時,需要考慮幾個編碼組件。當然,這取決於馬達的驅動方式,例如步進循環或微步進。
無論選擇哪種驅動方式,基本的步進馬達控制系統都需要特定的輸入和輸出。控制輸入通常是速度或位置(或兩者兼有)。另一個重要的輸入是已知頻率的時脈輸入,其他重要的控制器頻率將以此為基礎。對於單極馬達,輸出可以是每個繞組兩個開關位,對於雙極馬達,輸出可以是每個繞組四個開關位,但這可能會根據所選的馬達驅動硬體而有所不同。
步進循環
對於半步進或全步進步進馬達,控制系統是最簡單的。對於雙繞組馬達,該機器是四狀態或八狀態機,每個馬達有四個或八個輸出。
圖 3. 一個簡單的雙極步進馬達速度控制單元。
UPDOWN 計數器分別在前進為「1」或「0」時遞增或遞減狀態。狀態變化的速率取決於速度值和系統基準時脈的頻率。MotorOutput 將變數狀態轉換為直接與圖 1 中的電晶體綁定的相關控制位元。
對於速度控制,需要一個加/減可變頻率計數器。鎖相迴路(PLL)無法提供足夠的頻率控制,因此很可能需要一個自訂時脈或計數器控制單元。產生新時脈的簡單方法是使用重置計數器,其持續時間與預期速度成反比。以下程式碼片段展示了一個基於速度和方向輸入推進狀態變數的簡單過程。
PROCESS (clk)
VARIABLE t :INTEGER RANGE 0 TO 2097151:= 0;
CONSTANT dividend :INTEGER RANGE 0 TO 1048575:= 498047;
BEGIN
IF (clk'EVENT AND clk='1') THEN
IF (speed > 0) THEN
--t increments at the same frequency of clk and corresponds with
--how much time (in periods of clk) is taken before state is
--incremented. Speed, in short, increases how fast speed*t
--increments and changes how quickly states are stepped through.
t := t + 1;
IF (CONV_INTEGER(speed)*t >= dividend) THEN
t := 0;
--The following 5 code lines either increment or decrement the state.
--With only 4 or 8 states needed, a nice round 2 or 3 bit number
--will suffice for state and automatically roll over from 0
--to the highest value or visa versa. Also, if state is expanded
--beyond the two or three bits its entire value is representative of
--the motor’s position where the 2 or 3 least significant bits are
--all that are needed to control the current through the windings.
--The bit forward represents which direction the motor should turn.
IF (forward = '1') THEN
state <= (state + 1);
ELSE
state <= (state - 1);
END IF;
END IF;
END IF;
END IF;
END PROCESS;
恆定被除數由以下公式決定:
當中 (resolutionofspeed - 1) 等於速度允許的最大數值。
對於位置控制,狀態變數可以方便地擴展到所需的四到八個步長(這恰好對應於任何二進制數的前兩位或三位),從而更全面地了解馬達的當前位置。除了增加位置資料範圍外,還需要一個單獨的控制單元來控制馬達步進到其目標位置。以下範例是實現此目的的簡單方法:
PROCESS(clk)
VARIABLE t :INTEGER RANGE 0 TO 2097151:= 0;
CONSTANT dividend :INTEGER RANGE 0 TO 1048575:= 498047;
BEGIN
IF (clk'EVENT AND clk='1') THEN
IF (speed > 0) THEN
t := t + 1;
IF (CONV_INTEGER(speed)*t >= dividend) THEN
t := 0;
--the following SIGNAL position has replaced SIGNAL state and is
--meant to be far more than 2 or 3 bits
IF (forward = '1') THEN
position <= (position + 1);
ELSE
position <= (position - 1);
END IF;
END IF;
END IF;
END IF;
END PROCESS;
state <= position(2 DOWNTO 0);
---For half-stepping, 3 bits are used; for full-stepping, 2
speed <= '1' WHEN (position /= positionintended) ELSE '0';
forward <= '0' WHEN (position > positionintended) ELSE '1';
如果驅動負載具有較大的慣性,限制加速度可能是極為重要的問題。在這種情況下,如果加速度過大,馬達可能會滑動,導致開環位置或速度控制出現錯誤。解決這個問題的一個簡單方法是使用另一個加/減計數器,使實際轉速隨時間線性遞增;當預期速度大於目標速度時,實際速度遞增;當預期速度小於目標速度時,實際速度遞減:
圖 4. 實際速度根據預期速度安全地遞增和遞減。
請注意,速度增加和減少時的斜率不同;這對應於馬達加速和減速能力的差異。
PROCESS (clk)
VARIABLE t :INTEGER RANGE 0 TO 2097151:= 0;
CONSTANT accel :INTEGER RANGE 0 TO 2097151:= 390625;
CONSTANT decel :INTEGER RANGE 0 TO 2097151:= 195312;
BEGIN
IF (clk'EVENT AND clk = '1') THEN
t := t + 1;
IF (t > accel) THEN
IF (vactual < vintended AND vactual > 0) THEN
vactual <= vactual + 1;
t:=0;
ELSIF (vactual > vintended AND vactual < 0) THEN
vactual <= vactual - 1;
t:=0;
END IF;
END IF;
IF (t > decel) THEN
IF (vactual < vintended AND vactual < 0) THEN
vactual <= vactual + 1;
t:=0;
ELSIF (vactual > vintended AND vactual > 0) THEN
vactual <= vactual - 1;
t:=0;
END IF;
END IF;
END IF;
END PROCESS;
通常,可以透過假設馬達的加速度和減速度相同來簡化此編碼區隔。無論如何,常數加速度和減速度可以透過以下公式確定:
(2)
對於忽略位置的速度控制來說,這是一個很好的解決方案,但通常並不理想。對於加速度補償位置控制,一旦加速度變成非零,位置與速度就不再是線性關係,因此可能需要進行一些計算才能加速、以恆定速度滑行,並減速至在預期的最終位置完全停止。
使用前面提到的元素實現自適應加速度位置控制的一種方法是簡單地建立一條預期速度與位置曲線,以使實際速度趨近於預期減速度。忽略積分常數,並使用加速度、速度和位置的基本時間方程,我們可以得到以下結論:
(3)
(4)
使用常識可以得出預期速度和 ∆p 的以下關係,其中 ∆p 是預期位置 - 當前位置:
(5)
圖 5. 使用速度逼近演算法安全地移動到最終目標位置的速度和位置參數表示。
此解決方案的一個固有問題是,為了確保函數隨時間連續,實際速度必然落後於目標速度。另一個問題是需要將目標速度曲線與限制速度的減速度相匹配,因為不匹配會導致系統出現過阻尼或欠阻尼現象。一種解決方案是,一旦目標速度與實際速度相交,就直接跟隨該方程,但這需要考慮額外的、可能非常複雜的編碼。
這種加速度補償位置控制解決方案的優點之一是其故障安全保護。有了它,可以在到達最終位置之前的任何時間安全地即時更改預期最終位置,而無需重新計算位置與時間的關係,也無需完成移動到先前的預期位置。
從一個位置移動到另一個位置的更常見方法是使用馬達位置資料和馬達的預期最終位置來計算步進之間的停頓時間。當涉及位置控制時,系統在動態決策變更方面並非最佳選擇,但在需要精確控制且決策變更不成問題(遵循預定指令)時,系統非常適用。在這種情況下,為了確保恆定的加速度而用於遞增和遞減速度的計數器並不理想,因為兩個變數基於時間以不同的方式遞增可能會導致系統位置出現一些誤差。
如果需要一個簡單的點對點控制系統,並假設馬達在執行新指令之前保持忙碌狀態並停止,則可以使用簡單的近似公式:
(6)
Δt 是步驟之間所需的等待時間,Δx 是一個常數,等於馬達每次狀態變化時的移動量,s(速度)可以計算如下,其中 Δp 是目標位置 - 當前位置,Δn 是初始位置 - 目前位置:
(7)
圖 6. 點對點運動的速度與位置曲線。
可以建立一個計數器,等待必要的時間,然後朝著目標位置的方向進行相應的步進。此外,應注意 Δn 應略微偏移,使其不為零。
微步進
使用微步進驅動步進馬達的原因有很多,更高的精度和更低的共振效應(步進頻率與機械負載振動頻率匹配的抑制效果)只是其中兩個。只需進行一些添加和修改,即可利用先前的設計元素輕鬆實現微步進。
對於純開環馬達控制,脈寬調變(PWM)是改變馬達繞組時間平均電流的有效方法。因此,本文將討論一種 PWM 生成電路。
圖 7. PWM 單極步進馬達控制器的組件示意圖與簡單時序圖。
首先需要一個固定頻率的 PWM 基底計數器,其功能類似於用於模擬 PWM 產生的鋸齒波函數。計數器重設的頻率是主 PWM 頻率,而其遞增的頻率是基頻。主頻率應限制在 10KHz 到 30KHz 之間。較低的頻率會產生可聽噪音。較高的頻率會導致外部驅動器的功率效率逐漸降低,並可能產生大量相關的電磁干擾。基頻應等於主 PWM 頻率 x 脈寬解析度。此頻率可能不足以匹配正弦波中的步進狀態,但在如此高的頻率下,應考慮切換到全步進馬達的優勢。
計數器的輸出用作第二個附加元件的輸入:比較器組。它根據 PWM 值是大於還是小於另一個輸入值來控制切換。
另一個邏輯元件是正弦函數或查找表。對於此應用,查找表可以節省時間、處理能力以及低解析度晶片空間,而這些解析度對於微步進馬達控制來說綽綽有餘。輸入解析度決定了每個正弦波的狀態數,輸出解析度與脈衝寬度的解析度相同。此元件的輸出是比較器元件的正弦值。
由於每個繞組的扭矩與旋轉位置曲線並非完美的正弦曲線,因此使用完美的正弦查找表並非總是最佳解決方案。此外,對於繞組上施加的不同電壓,曲線的形狀並不總是相同的。為了提高馬達微步進的精度,可以修改此正弦曲線表,以補償馬達扭矩與旋轉位置曲線的缺陷。在以下等式中,n 是從 0 到 StatesPerSinusoid -1 的整數,K 是某個通常小於 1 的實數,可以對其進行修改,直到曲線為控制器提供足夠的精度。此技術是一種快速修復方法,不能保證始終有效,但通常可以在低步進頻率下提供肉眼可見的改善。
(8)
先前的加/減計數器仍然可以使用,但必須重新計算常數被除數,因為現在需要循環的狀態超過四個或八個。公式 1 仍然可以使用。
需要注意的是,PWM 控制的微步進在馬達轉速較高時,其精確度和適用性會逐漸降低。一旦馬達的電感特性開始占主導地位,正弦 PWM 就不會產生完全正弦的電流流過繞組,轉子的實際位置在接近滑差點時會滯後大約一整步。此外,由於步進循環會導致流過繞組的平均電流更高,因此它可以驅動馬達的速度略快於微步進本身的速度。
閉環電流控制器
通常情況下,步進馬達連接到過高的電壓電源,以補償馬達的電感特性,從而使馬達速度更快、更靈敏。這意味著需要某種形式的電流限制,而選擇的工具通常是外部截波電路。
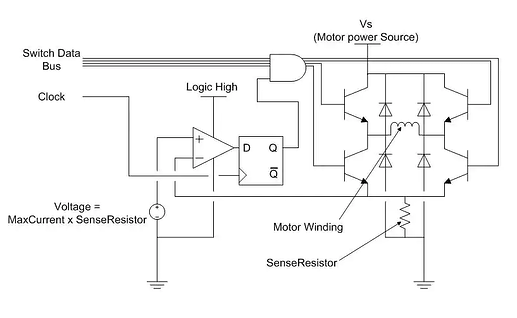
圖 8. 可行的限流硬體設定。
閂鎖的 Q-bit 與開關資料匯流排的每條線路進行「AND」運算,因此各「AND」閘的匯流排輸出寬度相等。
使用基於硬體的電流截波器控制步進馬達的唯一區別在於,它放棄了 PWM 生成,轉而採用微步進。簡單的循環步進電路無論是否使用基於電流截波器的硬體驅動器都能正常運作,但微步進控制需要一種將實際馬達電流與預期正弦波查找表資料進行比較的方法。實現此目的的方法有很多,但最常見且最簡單的方法是使用數位類比轉換器(DAC)將正弦波資料輸出到外部比較器(取代圖 8 中的恆定偏壓源)。採樣率很重要,因為速度太慢的系統可能無法如預期循環。為了跟上正弦波資料輸出,DAC 必須以等於狀態進展頻率(通常不超過 30KHz)的速率轉換資料。
依循指令集
在許多情況下,例如多馬達協調控制,需要極其精確和協調的精密速度和位置控制,最佳解決方案可能是為馬達的每一步提供基於時間的指令。與其對最大速度和加速度進行硬編碼的安全考慮,不如在考慮這些限制的情況下產生指令。系統的計算可能更複雜,但可以確保馬達的位置在預定的時間和地點更精確地跟隨。考慮到這一點,很可能需要更多的記憶體。
範例
本應用筆記附帶兩個相同編碼的 VHDL 範例,用於加速度補償動態位置單極馬達控制系統。第一個資料夾包含為 ALTERA DE2 板(開發和教育)構成的完整 Quartus 專案。第二個資料夾僅包含元件和封裝 VHDL 程式碼的單獨文字檔案。
此程式碼能透過每步 64 個狀態的微步進控制一台每轉 100 步的雙繞組雙極馬達(例如 Portescap 的 42M100B1B)。控制系統將馬達在任一方向上的運轉速度限制為每秒最多四轉。馬達的加速速度也限制為每秒兩轉,減速速度也限制為每秒四轉。正弦曲線表已簡化,假設對稱性,並在公式 8 中使用 K = 0.7 進行變形以匹配馬達。
圖 9. 範例程式碼的示意圖。
在 ALTERA 的 DE2 開發板上,引腳分配對應於 pi 的開關陣列(預期位置)、clk 的 50MHz 時脈以及第一個通用 IO 介面左側的前四個引腳(用於馬達開關)。
可以使用任何 PLD,但係統設計時使用的 PLD 是 ALTERA DE2 開發板上的 Cyclone II EP2C35F672C6N,該開發板使用 50MHz 時脈。如果使用不同的基頻訊號,則必須更改某些常數,因此本應用筆記中的公式在程式碼的註解中重複出現。18-bit 位置輸入資料由 DE2 開發板上 18 個開關陣列的簡單位元表示提供,因此如果不使用 DE2 開發板,則需要另一種將 18-bit 二進位數傳送給 PLD 的方法。
圖 10. 範例馬達驅動電路原理圖。
結論
本文涵蓋了一些基於 VHDL 的簡單 PLD 步進馬達控制器的基本考慮因素。