← Previous Analog Bits - Modeling a Load Cell in SPICE
This article makes use of multiple instances of the previous article’s unamplified load cell SPICE model. It provides an analog front end circuit for a multiple load cell system in which the output of all the load cells must be combined and amplified, and works for both single and dual rail applications. The examples given will be for the combination of four load cells such as in the four corners of a platform for a weigh scale, planar center of gravity locator, or position tracker.
Three major circuit variants will be provided; a simple version with no calibration and fixed gain, a version that allows for manual individual calibration of the load cells with a fixed gain, and a version that allows for a fully digitally automated individual calibration of the load cells and gain.
The largest advantage of this sort of circuit lies in the calibration process, which allows for greatly improved system performance when using cheaper, poorly matched load cells. The basic idea is that for the extra cost of additional parts in the analog front end and the extra effort of developing and performing a calibration process a great deal of cost can be saved by using cheaper load cells, which are apt to be the most expensive component of the overall system.
The circuits and simulations given are meant to provide a template for this sort of a circuit rather than a specific solution or complete BOM for any particular situation. As such, the examples were designed to be as broadly applicable as possible. Noticeably absent from all the circuits is any sort of filtering or other components for noise mitigation. Being a generic circuit, only a few basic suggestions and best practices can be discussed, as the necessary frequency response and noise reduction are inherently specific to an application.
Nearly all the simulations provided use the load cell parameters for the Measurement Specialties FX1901-0001-0100-L, with any specific assumptions or deviations noted in the respective section.
When the Load Cells Are Well Matched
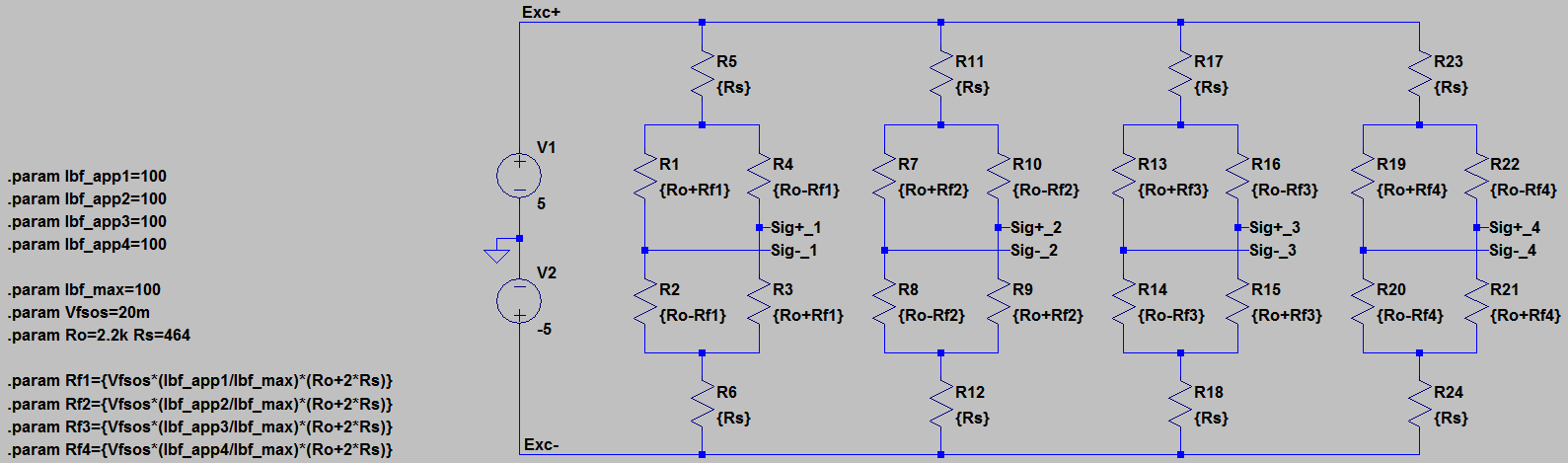
The problem is a lot simpler to solve if it can be assumed that the load cells used in the system will always be well matched in terms of their voltage output and impedance, but such load cells are apt to be much more expensive than what can be typically purchased off the shelf. In an LTspice simulation, four well matched (perfectly matched actually) load cells can be modeled as shown below, including dual +/- 5V power rails for their excitation voltages.
So we start with the basic problem of how to go about combining (adding? averaging?) and amplifying the differential output signals of the four load cells. Arguably the most straightforward way would be to use four buffered, precision, differential input amplifiers, most likely very expensive instrumentation amplifiers, (or one or two with a digitally controlled differential path multiplexer front end), one for each cell, and then to connect all of the outputs to ADC inputs and combine them in the digital realm. However, this is an Analog Bits article, so naturally the goal will be to let the analog circuit handle as much of this as possible before converting to the digital realm. That likely means op-amp circuits, which makes analog engineers smile, and most everyone else cringe.
Additionally, since the objective is to measure and amplify small (possibly very small) voltages precisely, specifically precision op-amps will need to be utilized . This is repeated for additional emphasis, since it’s important to understand that using any old op-amp for a task like this isn’t wise and in many cases won’t work. PRECISION OP-AMPS WILL NEED TO BE UTILIZED . Precision op-amps are specifically designed for DC gain accuracy having low input offset voltage and low input bias current.
With this being the goal, what would be a way to accomplish the combination? Since small voltages are being dealt with, it would presumably be best to add them and then amplify them, yes?
Understanding Why Not to Use Op-Amp Voltage Adders
This may seem like a perfectly reasonable place to begin, at least at first, but what will be demonstrated and discussed here are the limitations and downfalls to this approach.
The first problem that needs solving is that the load cell output voltages are differential in nature, which would lend itself well to the previously mentioned instrumentation amplifier solution; however, with a little clever trickery it may be possible to find a solution using cheaper (relatively speaking) precision op-amps.
For the dual rail situation where the load cell outputs are well matched and differential about GND , consider the idea of adding all the positive signal outputs together with a summing amplifier (voltage adder), adding all the negative signal outputs together with another summing amplifier, and then taking the combined positive outputs and subtracting the combined negative outputs with a difference amplifier (voltage subtractor). Gain could be provided by either the summing amplifiers, the difference amplifier, or both (I show a version with both below for demonstration). Since at least three precision op-amps that are +/- 5V dual rail capable are necessary, the LT6005 quad, precision, rail-to-rail op-amps were selected.
Download LTspice Circuit - Analog_Combinator_Fail.asc (8.3 KB)
The circuit above has a gain of 5/4 in each summing amplifier, but since four equal voltages are being summed this effectively becomes a gain of 5. The difference amplifier also has a gain of 5, therefore making the overall gain 5 multiplied by 5 for a total 25. For the load cell outputs of 20 mV/V, with 10 volts total of excitation voltage, and a total gain of 25, this should provide a positive 5V output when all four load cells are maximally loaded. It doesn’t though, it’s about 500 mV short.
So what’s the problem? Why isn’t it providing the full 5V (or as near as the op-amp output will allow), at full load?
Suffering From a Lack of Buffering
The first problem here is that the summing amplifiers, which are a type of inverting op-amp circuit, do not provide a high impedance buffer for the load cell output signals. This is because inverting op-amp circuits have a signal path from their input to output around the amplifier’s negative input via the feedback resistor. From the perspective of each load cell, half of its differential output impedance is simply in series with each 10 kOhm input resistor, therefore skewing the actual gain of the summing amplifier circuits.
Download Mathcad File -Analog_Combinator_Fail.mcdx (6.3 KB)
In fact, if buffering weren’t an issue, it would technically be possible to use a single op-amp for a combined differential summing and difference amplifier circuit, but unfortunately that doesn’t buffer properly either. In this case below, the overall circuit gain is effectively 4 multiplied by 6 (4 equal load cells summed and an amplifier gain of 6) for a total of 24, so the expected output at full load would be 4.8V, but even with much larger resistances (i.e. better buffering) used in the circuit there is still an error of more than 50 mV.
Download LTspice Circuit -Analog_Combinator_Fail_2.asc (7.0 KB)
Download Mathcad File - Analog_Combinator_Fail_2.mcdx (6.3 KB)
If it were reasonable to use resistors in the Megaohm range, that would be great, but for practical amplifier circuits this usually isn’t reasonable due to errors introduced from things such as input bias currents and additional noise (even if SPICE says it’s okay, don’t believe it without trying it out in reality). Also note that the original circuit wouldn’t work well for single rail applications (the latter would, but the point is moot since the buffering problem still remains). For the original circuit to work with a single rail, it would have to sum the negative and positive outputs the same way; however, both would have a common mode voltage of about half the single rail excitation voltage. That means the op-amps would need their single power rail to be more than twice (1/2 multiplied by 4) the load cells excitation voltage to be able to provide the proper output. This isn’t impossible of course, but it’s darned inconvenient unless such a voltage is already freely available in the system (again, a moot point because of the buffering problem).
So if this doesn’t work, what’s another solution that will properly buffer and without having to worry about higher voltage rails for the op-amps than the load cells in the single rail case?
Using Op-Amp Voltage Averagers Instead
A voltage averager is certainly a less well known op-amp circuit relative to a voltage adder. It’s really a special case of what this article refers to as a non-inverting summing amplifier (personally, I would call it a non-inverting weighted-averaging amplifier, that seems more mathematically accurate to me).
Although the algebra from the prior linked article is very messy at first glance, in the special case utilized here where all the input resistances are equal in value, all the inputs are actually just averaged (weighted the same) at the positive op-amp input prior to applying any gain. No gain is actually applied (a gain of 1) in these first examples so that they behave as simple voltage followers.
For Dual Rail Applications
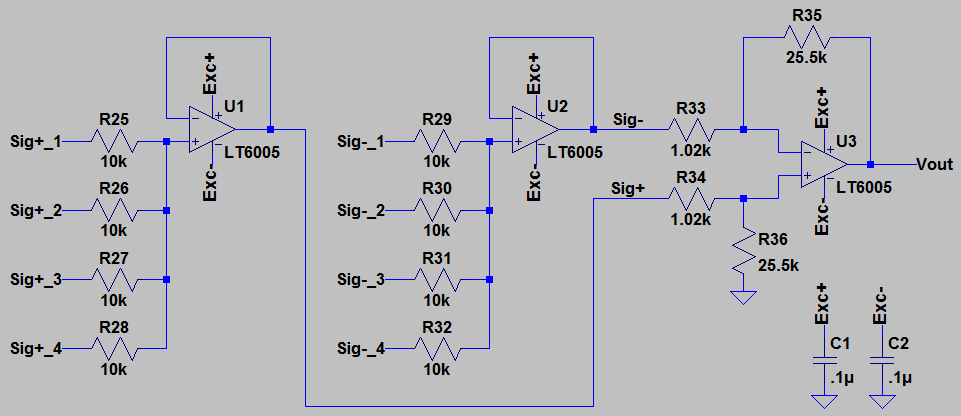
The problem of the load cell output voltages being differential in nature is solved in much the same way as the failed voltage adder circuit, with one op-amp handling the positive load cell outputs, another handling the negative load cell outputs, and another used for a difference amplifier. Once again the LT6005 quad, precision, rail-to-rail op-amps are used. The resistors in series with each load cell output will become more important later when dealing with load cells of greatly mismatched impedance, but for now just take it for granted that they should be there. The difference amplifier is set for a gain of 25 this time, which is also the overall gain since the voltage averagers have a gain of 1.
Download LTspice Circuit - Analog_Combinator_Win.asc (7.9 KB)
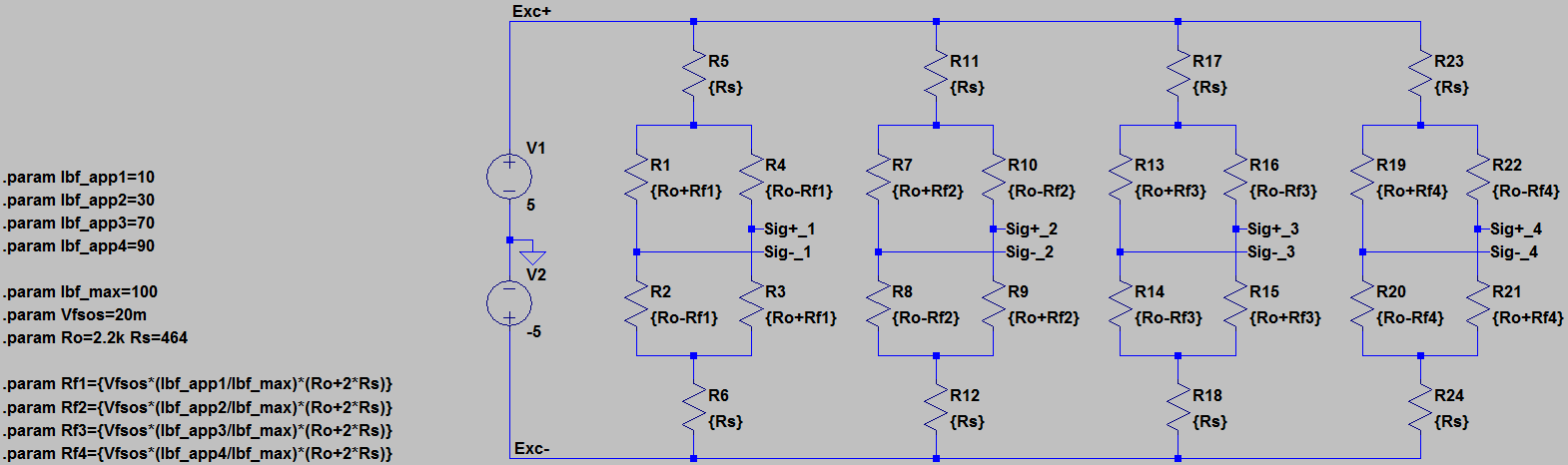
In the previous voltage adder failure examples all the load cells were loaded equally to show the circuits didn’t even work under that ideal situation, but in this case it’s convenient to show that not only does the circuit work, but works when the load cells have a great deal of variation in their loading (e.g. when an applied force is far off platform center of a weigh scale). Configuring the simulation as shown below with the load cells at 10, 30, 70, and 90 lbs for a sum total of 200 lbs should provide an output voltage of 2.5V.
Sure enough, it does, it’s little more than a mV off.
Download Mathcad File - Analog_Combinator_Win.mcdx (6.2 KB)
For Single Rail Applications
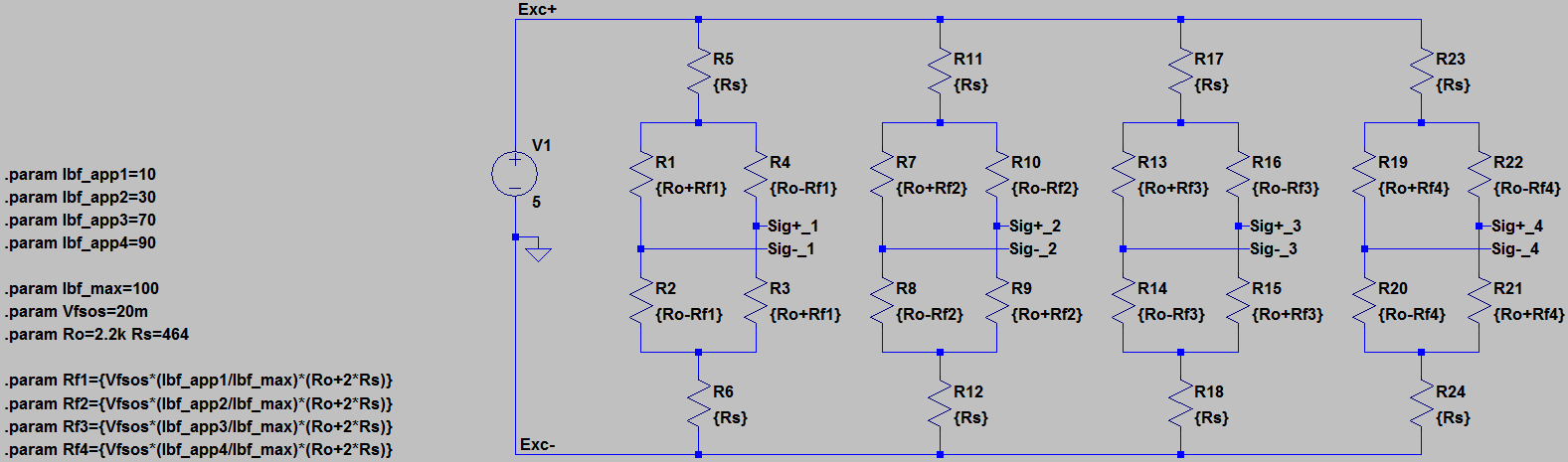
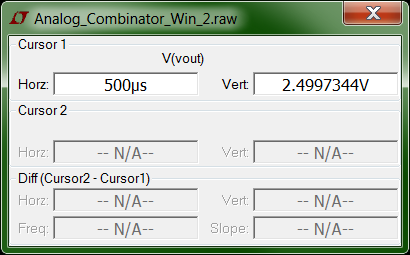
Here is another very nice benefit of this voltage averager method to accomplish the load cell output combination. It will actually also work with a single rail (assuming the selected op-amp will allow it of course), no other circuit changes are necessary beyond adjusting the difference amplifier gain to suit the difference in excitation voltage. Here going from dual +/- 5V rails to a single +5V rail (half the voltage) and doubling the difference amplifier gain yields nearly exactly the same result.
Download LTspice Circuit - Analog_Combinator_Win_2.asc (7.6 KB)
Download Mathcad File - Analog_Combinator_Win_2.mcdx (6.2 KB)
Note that the SPICE simulation doesn’t have any tolerances on the resistor values like there would be in the real world, and it would be recommended for accuracy of circuits like this to use matched resistor arrays rather than individual resistors. In the above circuit for example, the eight 10 kOhm input resistors could be provided by a single Y1103TR-ND array, and the four difference amplifier resistors by a single 541-3100-2-ND array. Understand that for accuracy the actual matching of the array resistors to each other is far more important than their absolute resistance tolerances.
When the Load Cells Aren’t Well Matched
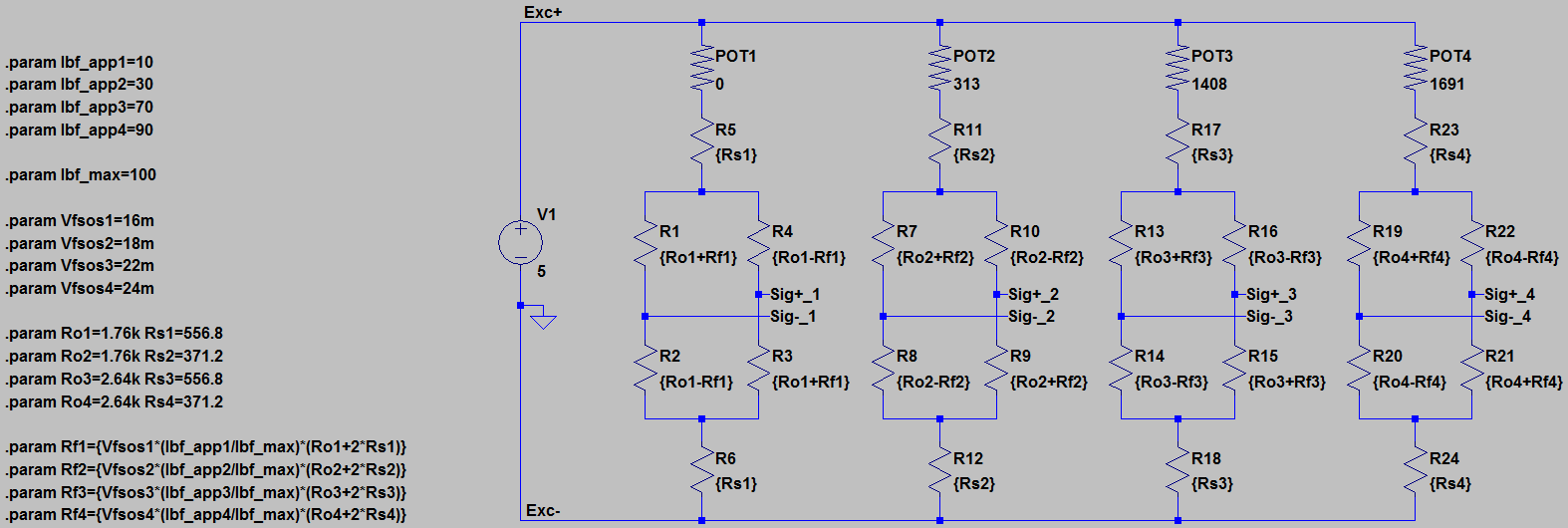
The problem is more complicated to solve if the load cells used in the system are poorly matched in terms of their voltage output and impedance, but such load cells are apt to be much cheaper and able to be purchased directly off the shelf. Note that from this point on, even though only single rail examples are shown, just as before this works with dual rails as well. In an LTspice simulation, four poorly matched load cells can be modeled as shown below, including a single 5V power rail for the excitation voltage and a potentiometer in series with each positive excitation lead of each load cell. Note that all the Ro and Rs values are now differentiated in the circuit and individually set along with Vfsos for each load cell, and the values vary +/- 20%.
Using Trimmer Potentiometers for Manual Calibration
The basic idea of calibration via the trimmer potentiometers shown above in each positive excitation lead of each load cell is to divide the excitation voltage down to a level such that the subsequent differential output voltage (mV/V Vfsos ) could be achieved by any variation in an individual load cell according to its datasheet ratings.
The potentiometer values shown above were set to provide equal differential output voltage matching of 16 mV/V for each load cell, and the best potentiometers to use would be multi-turn trimpots that could afford some degree of accuracy when being manually adjusted, such as 987-1809-2-ND. The simulation assumes that the potentiometer can go down to zero Ohms (the datasheet says 2 Ohms max) and that tuning resolution of 1 Ohm could be achieved, and that likely doesn’t reflect reality, but in this case it’s just for a proof of concept demonstration of the circuit and it’s convenient for the math to work out nice and evenly (or as evenly as the 1 Ohm resolution allows anyway).
A few additional circuit changes were made here compared to the previous successful demonstration for well matched load cells.
- Since only low voltage single rail cases will be shown going forward, even higher performance LTC2052 quad, precision, rail-to-rail, zero-drift (chopper stabilized) op-amps are used.
- The input resistors for the load cell signal outputs have been increased to 100 kOhm (e.g. Y1104TR-ND) to better drown out the impedance variation between the individual load cells (further explanation below).
- An additional very small amount of gain (because it must be very small, also further explained below) has been added to both the voltage averager stages (could be accomplished as shown with a single 541-3088-2-ND).
- A mechanism to disconnect the load cell signal outputs is included as a convenience for the simulation, so the load cells can be more easily individually calibrated (this could be real, also further explained below).
Download LTspice Circuit - Analog_Combinator_Win_3.asc (11.3 KB)
The input resistors being increased from 10 kOhm to 100 kOhm, as mentioned, is so that the variations in resistance of any one load cell relative to another are far less than the input resistors. This provides some very simple impedance matching of the load cells to each other. For example, in the case of +/- 20% for the nominal differential output impedance of the load cells of the above simulation, the difference between half the output impedance -20% and half the output impedance +20% (i.e. the worst case) would be 440 Ohms, which is less than 0.5% of each nominally 100 kOhm input resistor. This is important because any mismatch in impedance skews the result away from an equal averaging circuit and can give some load cells more weight in the average than others. Note that increasing the input resistors too high can actually have an adverse effect as they will introduce not only noise, but also DC error in to the circuit that’s dependent upon the op-amp input bias current. Here, for the LTC2052 with a maximum input bias current of +/- 150 pA, and four 100 kOhm resistors in parallel, the maximum error would be 150 pA multiplied by 25 kOhm for 3.75 uV, so very low. With sufficiently limited bandwidth via filtering (discussed more later, and depends on the application), the thermal noise introduced by the resistors can be kept in a similar very low single-digit uV range.
The very small amount of gain included in the op-amp averager input stages makes it a gain of roughly 5/4 instead of 1. This was added for both a demonstration that it can be done if desired, and because it made the overall fixed circuit gain work out very close to exactly as desired (a gain of about 51.25) with the real parts 541-3088-2-ND and 541-3100-2-ND. There is a very large caution here though. The gain of the averager stage would always have to be less than around 2, enough less that the average input voltage multiplied by the gain doesn’t exceed the output voltage limitation of the op-amp (or input limitation of the difference amp stage), and it’s important to remember that for a single rail system there is a large (around half of the excitation voltage) DC common mode voltage in all the load cell signal outputs.
The eight voltage controlled switches and their associated pull-up resistor added to the simulation are strictly there for when calibrating the individual load cells, but depending upon the system design goals something to accomplish the same function could actually exist in the physical circuit, say four of FSA1257AL8XTR-ND, one for each pair of load cell signal outputs. In the simulation they are wired such that they are all either open or closed at the same time, but they could be set up with individual control as well if desired (and required for planar center of gravity locator or position tracker applications).
Measurement during calibration via the trimmer potentiometers could be accomplished in multiple ways, but the simplest method is proposed here.
- Apply a known weight to the system with its planar center of gravity at platform center.
- Do one of the following where the disconnect in the system could be either directly via connector, effectively via jumper placements or switch settings, or effectively via digital switches:
- Either disconnect all four pairs (signal +/-) load cell outputs.
- Or disconnect all but one pair of load cell outputs.
- With a calibrated precision voltmeter do one of the following:
- Either measure each differential pair of signal outputs of each cell with all of them disconnected and adjust each trimmer potentiometer to achieve the desired reduced differential output at weight.
- Or measure the circuit’s final Vout when each load cell’s signal outputs are individually connected alone and adjust each trimmer potentiometer to achieve the desired output voltage at weight.
- Or do the same as b, but instead of using a voltmeter use the system’s internal measurement, presumably via an ADC and microcontroller.
- Reconnect all the load cells simultaneously and confirm that the measurement for the calibration weight hasn’t changed appreciably.
- Optional for weigh scales: move the applied weight’s planar center of gravity around on the system’s platform and confirm that the measurement hasn’t changed appreciably.
- For a planar center of gravity locator or position tracker: verify that the system can measure those things to the required accuracy.
Note that the planar center of gravity locator or position tracker options require that the system be able to individually measure each load cell’s output (say using four microcontroller GPIO and four FSA1257AL8XTR-ND) so that the necessary trigonometry could be done using all the outputs to determine location on the system platform. Also note, that the options for b and c of steps 2 and 3 above are best since the calibration is being done on the overall system result, and with larger voltages which are easier to measure with lower error.
Since it’s easy to accurately measure small differential output voltages in SPICE, option a was used in steps 2 and 3 above in the simulation, and the results still work out well as before.
Download Mathcad File - Analog_Combinator_Win_3.mcdx (6.2 KB)
Using Digital Potentiometers and Rheostats for Automatic Calibration
The same basic idea of manual calibration by trimmer potentiometers in each positive excitation lead of each load cell can be accomplished by digital rheostats instead. Again, the goal is to divide the excitation voltage down to a level such that the subsequent differential output voltage (mV/V Vfsos ) could be achieved by any variation in an individual load cell according to its datasheet ratings. Unlike the previous manual load cell calibration with fixed gain circuit, the mV/V Vfsos selected for matching could be a static number for all units of a produced product based on the worst case expectation from the load cells used, or it could be different for each unit built if the implemented gain calibration always just tunes the other three load cells down to whichever load cell reads the lowest naturally. The latter only works in this case because the gain can be adjusted accordingly to match, as will be seen.
The rheostat settings shown below were set to provide equal differential output voltage matching of 15 mV/V for each load cell if four AD5174BCPZ-10-RL7TR-ND, 10 kOhm, 1024 tap rheostats are used and worst case maximum (according to the datasheet) values are used for their wiper resistance and total resistance tolerance. The AD5174BCPZ-10-RL7TR-ND is also SPI bus controlled and non-volatile, which is also convenient for holding calibration between power cycles without the system having to do anything else.
Low wiper resistance is desirable because it effectively sets the minimum resistance that the rheostat can achieve, and 10s of Ohms can be a lot of additional unavoidable resistance undesirably dividing off excitation voltage for something like a 350 Ohm load cell (this is demonstrated later). Low total resistance itself is unimportant as long as there isn’t too little to divide down the excitation voltage as desired for the application; however, as the total resistance increases for the same amount of available digital rheostat tap settings the effective tuning resolution decreases. So the digital rheostat used must have low enough wiper resistance, sufficiently high total resistance, and sufficient tuning resolution for a given application. The AD5174BCPZ-10-RL7TR-ND was selected because it’s a very high-end digital rheostat with very low wiper resistance (70 Ohms max), nominally 10 kOhm but +/- 15% total resistance (enough for even high impedance load cells like the FX1901-0001-0100-L), and excellent tuning resolution despite the high total resistance via it’s 1024 available tap settings (affording tuning resolution of about 10 Ohms). The SPICE simulation includes the 70 Ohms wiper resistance and 11.5 kOhm (10 kOhm +15%) total resistance to provide a worst case for both minimum resistance and tuning resolution.
A few additional circuit changes were made here compared to the previous successful demonstration for poorly matched load cells with manual calibration.
- The averager stage gain has been eliminated (gain of 1) by making them voltage followers again.
- The mechanism to disconnect the load cell signal outputs can connected/disconnected them in individual pairs via GPIO (four FSA1257AL8XTR-ND could still be used in reality).
- The fixed resistors of the difference amplifier stage have been replaced by two digital potentiometers (further explanation below).
- An additional non-inverting gain stage has been added, with a gain that is also controllable via a digital potentiometer (further explanation below).
Download LTspice Circuit - Analog_Combinator_Win_4.asc (13.1 KB)
The use of two potentiometers in the difference amplifier stage is nice for multiple reasons. Since it’s really just the ratio that matters, and even overall resistance value matching between the positive and negative sides is unimportant, the exact resistance values and tolerances are relatively unimportant as long both potentiometers are given the same setting. Since the wiper resistances are just in series with the positive and negative op-amp inputs, wiper resistance effectively doesn’t matter. In fact, as long as the nominal resistance matching between both sides to the wiper is accurate, the ratio will be similarly accurate, and this doesn’t even take a particularly expensive potentiometer. For example a single MCP4341T-103E/ML-ND quad, 10 kOhm, 129 tap, potentiometer could be used for both the difference amplifier pots and the next non-inverting gain stage pot. Don’t be confused by the 129 taps number, there are 128 digital settings via 7-bits, but also note that because a gain of less than 1 would never be desirable only half of the settings are available for the difference amplifier stage (they are all available for the non-inverting stage though). The MCP4341T-103E/ML-ND is also SPI bus controlled and non-volatile (same as the AD5174BCPZ-10-RL7TR-ND), which is also convenient for holding calibration between power cycles without the system having to do anything else.
The added non-inverting amplifier gain stage is optional, but since a fourth op-amp is apt to be available in the same package as the other three of the system (assumes a quad op-amp) it adds flexibility for very little added unit cost (added cost for needing an additional potentiometer). It may actually make more sense from a symmetry and noise perspective and for ultimately better system accuracy to make this another difference amplifier stage (another unused potentiometer is already available if using a quad pot) that just happens to have the negative side connected to GND . That consideration is elaborated on more in the noise and thermoelectric effect error considerations section, but it has the disadvantage of limiting the number of possible gain settings to half the number of taps, as was previously mentioned. The simulation here just uses a basic non-inverting amplifier stage, and the higher the earlier difference amplifier stage gain is the less the error caused by noise and thermoelectric effects will be for the non-inverting amplifier stage anyway. This second gain stage is especially useful in a system that needs to amplify very small voltage output load cells, say a 2 mV/V Vfsos type cell.
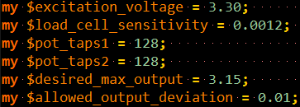
Since the simulation this time is calibrating each mismatched load cell down to 15 mV/V Vfsos output, and there are two gain stages, the question becomes what maximum output voltage is desired and how should the two gains be set to achieve this when all the load cells are at maximum capacity. Frankly, I’m lazy (in this case the good engineering kind of lazy), so I wrote a quick script in Perl to figure this out based on the parameters entered at the top of the program. Here it is below along with a download, but even if you don’t use or want to install Perl it’s not something that would be particularly hard to recreate in any reasonable language.
Download Perl Script - TwoStageGainCalc.pl (2.2 KB)
And this as is produces the following output.
It’s arguably best for noise and thermoelectric effect considerations to put as much gain as possible in to the difference amplifier stage, but in the simulation’s case which doesn’t account for such things the difference amplifier and non-inverting amplifier potentiometer settings were selected as 16 and 14 respectively (as shown in the circuit above for Pset1 and Pset2 ) to give exactly 4.8V output nominally at full load. With the same uneven loads as before of 10, 30, 70, and 90 lbs for 200 lbs total, the output should be half that voltage, or 2.4V, and sure enough.
Download Mathcad File - Analog_Combinator_Win_4.mcdx (6.2 KB)
The 15 mV/V and 4.8V maximum output voltage were admittedly selected to make this work out near perfectly given the specific load cell mismatches and afforded tuning resolution of the digital rheostats. There are unfortunately more non-ideal effects to account for in the real world. Also, the 4.8V maximum output is a much more conservative figure for the LTC2052 op-amp (the datasheet specifies 150mV from the positive rail worst case for a 2 kOhm output load).
The other large advantage of doing the load cell matching and gain adjusting with digitally controlled rheostats and potentiometers is alluded to in the title of this section. It’s possible to fully automate this calibration, either at the end of the manufacturing line, in the field if regular re-calibration is necessary, or both. All that’s needed is a known weight that can be centered on the system’s load platform (in certain cases this could literally just be the inherent weight of the platform or entire product), and a programmed calibration algorithm which could be written in many different ways. The calibration could be initiated manually, automatically, or both depending on the system’s complexity. Of course, fully automatic calibration would be a bad idea if the business model for the company making the product depends on expensive, regular re-calibration period service calls. ![]()
The Ultra-Low Voltage Low Load Cell Impedance Challenge
The circuit is admittedly more challenged by ultra-low voltage low load cell impedance applications. It’s really made to work better for the higher impedance, higher output voltage, but poorly matched cheaper load cells like the previously simulated FX1901-0001-0100-L. An ultra-low voltage application can work though… well, at least theoretically in a SPICE simulation, real world proof would require real world testing (that’s just a truism though). Here, for a worst case test, a single 3.3V rail will be used, and some fairly outlandish assumptions are made for an imaginary load cell. It will have a 350 Ohm output impedance, 2 mV/V Vfsos output, and +/- 20% tolerance for both impedance and output voltage. That’s really bad tolerance for that voltage and impedance, hopefully no manufacturer makes a load cell like this, but it will make for a good theoretical worst case test of the circuit’s SPICE simulation. Also, in the simulation below the compensation resistors have been effectively eliminated by making them all 1 mOhm, and the rheostats are set to try and calibrate to a common Vfsos of 1.2 mV/V. Yes, 1.2 mV/V is absurdly low (especially for a 3.3V single rail), but if the load cell is at -20% impedance, 280 Ohms, and the rheostat is at its worst case minimum, 70 Ohms (this is why a digital rheostat with low wiper resistance is so important), voltage division says that 1.28 mV/V is the worst case expected minimum and the load cells must be matched to that or lower, so 1.2 mV/V it is.
There are no other circuit changes here from before other than adjusting the potentiometers for a different (much higher) gain. Again, the previous Perl script was used to help determine the best potentiometer settings, with the parameters at the top changed as shown for the single 3.3V rail, 1.2 mV/V Vfsos , and a desired maximum output voltage of 3.15V (the rail less 150mV for the LTC2052 op-amp).
Which doesn’t leave much choice for settings.

So the difference amplifier’s potentiometers are set to 4 ( Pset1 ) and the non-inverting amplifier’s potentiometer to 5 ( Pset2 ) for a total gain of almost 800 (almost 60 dB), and the resulting target maximum output voltage is approximately 3.143V.
Download LTspice Circuit - Analog_Combinator_Win_4_Test.asc (13.1 KB)
The simulation again works out very closely for the same very imbalanced 200 lb total load condition as before.
Download Mathcad File - Analog_Combinator_Win_4_Test.mcdx (6.3 KB)
The first real difficulty of an ultra-low voltage low load cell impedance application like this comes in the load cell tuning. Since the minimum rheostat resistance can be relatively high compared to the load cell impedance due to wiper resistance, even for very high-end digital rheostats, that leaves less voltage to work with. Additionally, even though the rheostat tuning resolution is the same, each single digit change in a rheostat tap setting accounts for a lot more voltage being added/subtracted in the voltage division between the rheostat and the load cell, effectively making accurate tuning more difficult.
The other real difficulty of an ultra-low voltage application like this isn’t represented at all in the SPICE simulation. That is, error caused by noise and thermoelectric effects.
Noise and Thermoelectric Effect Error Considerations
To help understand the fundamentals of these problems, Keithley Application Note Number 200 explains them very well and very succinctly with some simple real world numbers included. Also, there are any number of online quick calculators for thermal noise introduced by the resistors (Johnson Noise). Books can, and have been written about these topics, along with many articles and application notes (here is a good and relevant example regarding noise), so this section attempts to limit its scope to how to best go about minimizing them for the given circuits. There are a number of basic rules that can be followed to achieve this.
Starting with thermal noise, the two main practical ways to reduce it as much as possible are fairly obvious based on the ![]() formula. Either reduce resistance values or reduce circuit bandwidth (since it’s likely impractical to refrigerate the circuit, in most cases anyway.
formula. Either reduce resistance values or reduce circuit bandwidth (since it’s likely impractical to refrigerate the circuit, in most cases anyway. ![]()
The input resistors for the averager stage of all the previously given working circuits are apt to be the main source of such error since they need to be made large enough relative to the load cell impedance variations to properly drown those variations out. This makes it a problem of selecting resistance values that minimize the overall error introduced by the combination of potential load cell impedance mismatches and thermal noise. The 100 kOhm values selected in the later circuits are a reasonable starting point for a generic circuit, but this could change depending on the load cells used, necessary bandwidth, and how much introduced noise is acceptable.
Limiting bandwidth can be relatively easy. None of the circuits in this article included any added filtering to do so, because the necessary bandwidth also depends heavily on the specific application. Noise reduction techniques, especially in regard to op-amps, is a topic that could fill a book all by itself, but even the most basic filtering afforded by a few well placed and correctly valued capacitors can be sufficient. Having multiple op-amp stages also affords the opportunity for multiple filter stages, which is a nice perk.
For the basic and easy, consider simply limiting the bandwidth by adding single-pole low-pass filtering to each stage. With three stages to work with, and setting the same pole frequency at each, this can give a 60 dB per decade filter cornered at the selected pole frequency for the application. For a circuit with fixed gain stages all this would take is equally valued capacitors at each positive op-amp input to GND of the averager stages, equally valued capacitors in parallel with the feedback resistor and its other value matched resistor to GND in the difference amplifier stage, and a capacitor in parallel with the feedback resistor of the non-inverting amplifier stage. For a circuit with adjustable gain stages (manual with trim pots or automatic with digital pots) it’s a little more complicated since the pole frequencies would of course shift as the potentiometer setting changed. In that case, if the single pole from the averager stages is insufficient, fixed capacitors could still be placed as indicated as long as this shifting pole frequency was understood and account for by the designer. Or, one gain stage could be fixed with the additional filtering and the remaining gain stage dynamically adjusted as necessary (a compromise for a two-pole system). A differential filter cap could also be added between the positive and negative inputs of the difference amplifier stage, or between each of the individual load cell signal positive and negative lines as well. The point is, the designer has ALL this versatility if they need it, and can do what makes the most sense for their specific application.
To limit the errors introduced by thermoelectric effects, in this case the solder joints between all the components and the PCB, the advice is much simpler. In fact, this advice applies for reducing other sources of noise error as well. Good PCB layout, and specifically for thermoelectric effects, as much symmetry of the PCB layout as possible is the general advice. Good PCB layout, yet another topic that can and does fill books, isn’t so complicated if the usual best practice rules for precision analog circuits are followed. Keep runs of traces as short as possible with as few vias (ideally zero) as possible, run differential pairs of lines with set spacing differentially, keep components of the same signal path in close proximity (especially filter components), keep nets that could cause coupling/interference physically far apart, make all the signal paths for each individual load cell as physically symmetric as possible, have the signal paths for the combined positive and combined negative signals run differentially and as symmetrically as possible, and if there are any heat sources in the circuit/system try to isolate the precision analog circuit from them (or at least share the heat as equally as possible).
Consider the inherent symmetry that is possible with the given circuits (all the way up to the non-inverting gain stage anyway), this can be a tremendous advantage in PCB layout. Making everything as symmetric as possible will take advantage of the difference amplifier stage, which due to the subtraction of the two averager outputs will actually cancel out these errors as long as the same amount of error is seen in both signal paths all the way up to the difference amplifier. Since the difference amplifier stage also includes gain, the lack of symmetry in the non-inverting gain stage matters less, which is why is was previously mentioned that having higher gain in the difference amplifier stage is likely preferable, or that otherwise it may make sense to make the non-inverting stage another difference amplifier stage (using the 4th unused potentiometer from the quad pot) that just happens to have one input connected to GND . These are just a few more degrees of freedom afforded to the designer.
Shouldn’t as Much as Possible of This Be Done Digitally Anyway?
Yes. That’s probably not the answer expected of an analog enthusiast, but I’m also a pragmatic engineer, and the reality of today’s electronics is that, yes, it likely makes sense to do as much of this in the digital realm as possible. In fact, many integrated circuits today essentially do all of these things for the user, and being much smaller and on silicon there are ways to reduce sources of error more than anyone outside the silicon could ever hope to. The only real advantages of the circuits given in this article are versatility for the designer, possibly speed, and possibly cost. Speed may not be true, since modern digital filtering in things like DSPs and even some microcontrollers can beat the inherent time delays introduced by analog filtering; of course, analog filtering could be neglected entirely and done digitally along with digital noise filtering on the back end for any solution. Cost really depends on how high end of an integrated circuit is being considered, and how costly the designer’s selected BOM of parts for the less integrated solution above would be. There is a lot of variation, and some all-in-one ICs can become quite expensive. Here are a couple of examples of integrated circuits to accomplish the same task.
The ADUCM361 could be used. Not only does it integrate a front end multiplexer (differential signal capable) that could handle all the load cell signal outputs, buffering, configurable gain of up to 128, and a 24-bit Sigma-Delta ADC with precision reference, but it also happens to include a complete microcontroller with a host of digital peripherals as well. The ADUCM360 is the same but includes two complete analog signal chains after the multiplexer and an additional 24-bit Sigma-Delta ADC for twice the throughput. This is of course more of a system-on-chip solution, and it would depend if the included microcontroller is a convenience or a drawback for the system in question. Is it the only microcontroller that would be needed in the system, or would it be just one more thing that would need to be programmed costing money during manufacturing, as well as costing money during software development?
The cheapest way found was the NAU7802SGI TR-ND. It would take two of them, or else an additional front-end differential multiplexer, but it integrates a dual-channel differential input multiplexer, buffering, configurable gain up to 128, and a 24-bit Sigma-Delta with on board reference and oscillator at a very low price. Undoubtedly nothing here is high-end, but if all that’s needed is a basic solution for the application, and the performance isn’t overly critical, the low price combined with the reduced system complexity is hard to ignore.