Learning Companion for the Resistive Voltage Divider

APDahlen · July 28, 2025, 6:22pm

This article is part of a guided learning series on voltage dividers.

Canonical Article: Voltage Divider Fundamentals

Purpose of This document

These questions may be assigned:

as homework
as an interactive group discussion
as part of an AI-directed learning exercise

Use of AI in the Classroom:

The AI can serve as a strong sounding board from which you can explore the questions. When used properly, it acts as Vygotsky’s MKO (More Knowledgeable Other), allowing you to stretch into that Zone of Proximal Development (ZPD) See this link for additional tips on the use of AI in the classroom.

Audience Key

The following emojis are used to classify each question with alignment to Bloom’s taxonomy:

Technicians – Factual, practical, and troubleshooting-focused
Students – Foundational understanding with basic application
Capstone students and field engineers – Open-ended analysis with emphasis on system-level design tradeoffs
Teacher – Topics suited for discussion groups or guided exploration

Questions for Anchored AI-Assisted Learning

This section contains a list of questions with answers to help you better understand the material.

1) What is the equation for the voltage divider?

Answer

2) Can a variable resistor be used as a voltage divider?

Answer

3) Construct and then solve five unique voltage divider problems.

Answers will vary.

Tech Tip: This question requires active learning where you frame the material, provide a solution, and then verify that the solution is correct. This action is considerably more effective than the overreliance on the plug-n-chug method often associated with introductory circuit analysis.

Learning is messy - lean into it and work with a classmate to see who can come up with the best questions. BTW, the best questions are the ones that look complex but are simple to solve without a calculator, provided you understand the technique.

4) What two equations are used to develop the voltage divider shortcut?

Total current is defined as:

I = \frac{V_{in}}{R_1 + R_2}

The voltage across the R2 output is defined as:

V_{R2} = I \times R_2

If we combine the equations, we see that:

V_{R2} = V_{out} = \frac{V_{in}}{R_1 + R_2} \times R_2

As a final step, we rearrange the equations to obtain the standard form of the voltage divider formula:

V_{out} = \frac{V_{in}\times R_2}{R_1 + R_2}

5) Locate the specifications for the voltmeter used in your lab. What is the input impedance?

Answers will vary.
You are encouraged to verify your work using DigiKey’s voltage divider calculator.
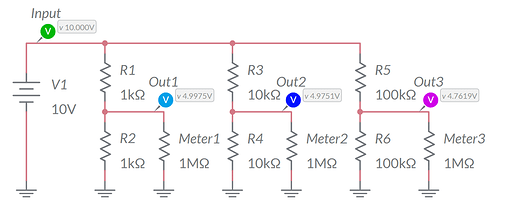
Finally, you are encouraged to build a circuit to demonstrate circuit loading. I have used this simple circuit (below) with excellent results in the lab. This is also an excellent launching point into Thévenin equivalent circuits.

6) With regard to the previous question, recalculate using the specifications for a classic analog meter of your choice.